Page 139 - 22825_Fulltext

3-2

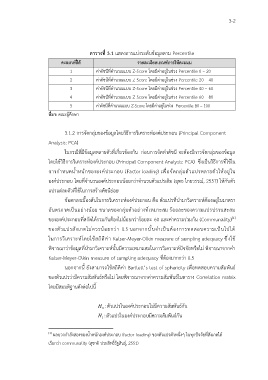
ตารางที่ 3.1 แสดงการแบ่งระดับข้อมูลตาม Percentile
คะแนนที่ได้ รายละเอียดเกณฑ์การให้คะแนน

1 ค่าดัชนีที่คำนวณแบบ Z-Score โดยมีค่าอยู่ในช่วง Percentile 0 – 20
2 ค่าดัชนีที่คำนวณแบบ Z-Score โดยมีค่าอยู่ในช่วง Percentile 20 – 40

3 ค่าดัชนีที่คำนวณแบบ Z-Score โดยมีค่าอยู่ในช่วง Percentile 40 – 60
4 ค่าดัชนีที่คำนวณแบบ Z-Score โดยมีค่าอยู่ในช่วง Percentile 60 – 80
5 ค่าดัชนีที่คำนวณแบบ Z-Score โดยมีค่าอยู่ในช่วง Percentile 80 – 100

ที่มา: คณะผู้ศึกษา

3.1.2 การจัดกลุ่มของข้อมูลโดยวิธีการวิเคราะห์องค์ประกอบ (Principal Component
Analysis: PCA)

ในกรณีที่มีข้อมูลหลายตัวที่เกี่ยวข้องกัน ก่อนการจัดทำดัชนี จะต้องมีการจัดกลุ่มของข้อมูล

โดยใช้วิธีการวิเคราะห์องค์ประกอบ (Principal Component Analysis: PCA) ซึ่งเป็นวิธีการที่ใช้ใน
การกำหนดน้ำหนักขององค์ประกอบ (Factor loading) เพื่อจัดกลุ่มตัวแปรหลายตัวให้อยู่ใน

องค์ประกอบ โดยที่จำนวนองค์ประกอบน้อยกว่าจำนวนตัวแปรเดิม (ยุทธ ไกยวรรณ์, 2557) ให้กับตัว

แปรแต่ละตัวที่ใช้ในการสร้างดัชนีย่อย
ข้อตกลงเบื้องต้นในการวิเคราะห์องค์ประกอบ คือ ตัวแปรที่นำมาวิเคราะห์ต้องอยู่ในมาตรา

อันตรภาคเป็นอย่างน้อย ขนาดของกลุ่มตัวอย่างที่เหมาะสม ร้อยละของความแปรปรวนสะสม

ขององค์ประกอบที่สกัดได้รวมกันต้องไม่น้อยกว่าร้อยละ 60 และค่าความร่วมกัน (Communality) [1]
ของตัวแปรสังเกตไม่ควรน้อยกว่า 0.5 นอกจากนั้นจำเป็นต้องการทดสอบความเป็นไปได้

ในการวิเคราะห์โดยใช้สถิติค่า Kalser-Meyer-Olkin measure of sampling adequacy ซึ่งใช้

พิจารณาว่าข้อมูลที่นำมาวิเคราะห์นั้นมีความเหมาะสมในการวิเคราะห์ปัจจัยหรือไม่ พิจารณาจากค่า
Kalser-Meyer-Olkin measure of sampling adequacy ที่ต้องมากกว่า 0.5

นอกจากนี้ ยังสามารถใช้สถิติค่า Bartlett’s test of sphericity เพื่อทดสอบความสัมพันธ์

ของตัวแปรว่ามีความสัมพันธ์หรือไม่ โดยพิจารณาจากค่าความสัมพันธ์ในตาราง Correlation matrix
โดยมีสมมติฐานดังต่อไปนี้

H 0 :ตัวแปรในองค์ประกอบไม่มีความสัมพันธ์กัน

H 1 :ตัวแปรในองค์ประกอบมีความสัมพันธ์กัน

[1] ผลบวกกำลังสองของน้ำหนักองค์ประกอบ (factor loading) ของตัวแปรตัวหนึ่งๆ ในทุกปัจจัยที่สังเกตได้
เรียกว่า communality (สุชาติ ประสิทธิ์รัฐสินธุ์, 2551)