Page 62 - kpi19903

36

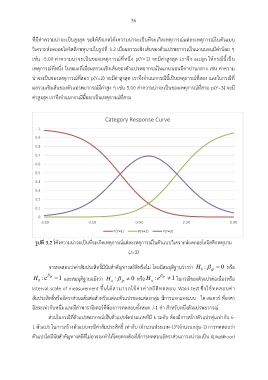
ที่มีค่าความน่าจะเป็นสูงสุด ขอให้สังเกตโค้งความน่าจะเป็นที่จะเกิดเหตุการณ์แต่ละเหตุการณ์ในตัวแบบ
วิเคราะห์ถดถอยโลจิสติกพหุนามในรูปที่ 3.2 เมื่อผลรวมเชิงเส้นของตัวแปรพยากรณ์ในแกนนอนมีค่าน้อย ๆ

เช่น -5.00 ค่าความน่าจะเป็นของเหตุการณ์ที่หนึ่ง p(Y=1) จะมีค่าสูงสุด เราจึง assign ให้กรณีนี้เป็น

เหตุการณ์ที่หนึ่ง ในขณะที่เมื่อผลรวมเชิงเส้นของตัวแปรพยากรณ์ในแกนนอนมีค่าปานกลาง เช่น ค่าความ
น่าจะเป็นของเหตุการณ์ที่สอง p(Y=2) จะมีค่าสูงสุด เราจึงจ าแนกกรณีนี้เป็นเหตุการณ์ที่สอง และในกรณีที่

ผลรวมเชิงเส้นของตัวแปรพยากรณ์มีค่าสูง ๆ เช่น 5.00 ค่าความน่าจะเป็นของเหตุการณ์ที่สาม p(Y=3) จะมี

ค่าสูงสุด เราจึงจ าแนกกรณีนี้ออกเป็นเหตุการณ์ที่สาม

Category Response Curve

1

0.9
0.8
0.7

0.6
0.5

0.4
0.3

0.2
0.1

0
-5.00 -2.50 0.00 2.50 5.00

P(Y=1) P(Y=2) P(Y=3)

รูปที่ 3.2 โค้งความน่าจะเป็นที่จะเกิดเหตุการณ์แต่ละเหตุการณ์ในตัวแบบวิเคราะห์ถดถอยโลจิสติกพหุนาม

(J=3)

การทดสอบว่าค่าสัมประสิทธิ์มีนัยส าคัญทางสถิติหรือไม่ โดยมีสมมุติฐานว่างว่า H 0 :   หรือ
0
jp
H 0 :e  jp  1 และสมมุติฐานแย้งว่า H a :   หรือ H a :e  jp  1 ในกรณีของตัวแปรต่อเนื่องหรือ
0
jp
Interval scale of measurement ขึ้นได้สามารถใช้ค่าค่าสถิติทดสอบ Wald test ซึ่งใช้ทดสอบค่า
สัมประสิทธิ์หรืออัตราส่วนแต้มต่อส าหรับแต่ละตัวแปรของแต่ละกลุ่ม มีการแจกแจงแบบ ไค-สแควร์ ที่องศา

อิสระเท่ากับหนึ่ง และมีค่าพารามิเตอร์ที่ต้องการทดสอบทั้งหมด J-1 ค่า ส าหรับหนึ่งตัวแปรพยากรณ์

ส่วนในกรณีที่ตัวแปรพยากรณ์เป็นตัวแปรจัดประเภทที่มี k ระดับ ต้องมีการสร้างตัวแปรหุ่นเท่ากับ k-
1 ตัวแปร ในการสร้างตัวแบบจะมีค่าสัมประสิทธิ์ เท่ากับ (จ านวนประเภท-1)*(จ านวนกลุ่ม-1) การทดสอบว่า

ตัวแปรใดมีนัยส าคัญทางสถิติไม่อาจจะท าได้โดยตรงต้องใช้การทดสอบอัตราส่วนภาวะน่าจะเป็น (Likelihood