Page 61 - kpi19903

35

Operating Characteristic Curve
1

0.9
0.8
0.7
0.6
0.5

0.4
0.3
0.2
0.1
0
-5.00 -2.50 0.00 2.50 5.00
Y=3 Y=2

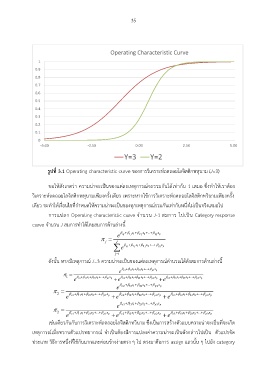
รูปที่ 3.1 Operating characteristic curve ของการวิเคราะห์ถดถอยโลจิสติกพหุนาม (J=3)

ขอให้สังเกตว่า ความน่าจะเป็นของแต่ละเหตุการณ์จะรวมกันได้เท่ากับ 1 เสมอ ซึ่งท าให้เราต้อง

วิเคราะห์ถดถอยโลจิสติกพหุนามเพียงครั้งเดียว เพราะหากใช้การวิเคราะห์ถดถอยโลจิสติกทวินามเพียงครั้ง

เดียว จะท าให้เงื่อนไขที่ก าหนดให้ความน่าจะเป็นของทุกเหตุการณ์รวมกันเท่ากับหนึ่งไม่เป็นจริงเสมอไป
การแปลง Operating characteristic curve จ านวน J-1 สมการ ไปเป็น Category response

curve จ านวน J สมการท าได้โดยสมการด้านล่างนี้


... 
x
e    1 j x  2 j x   pj p
oj
2
1
 
j J
 e    1 j x  2 j x   pj p
... 

x
oj
1
2
j 1
ดังนั้น หากมีเหตุการณ์ J=3 ความน่าจะเป็นของแต่ละเหตุการณ์ค านวณได้ดังสมการด้านล่างนี้
e o  1  11 1 x  21 2 ...x    p 1 p x
 
1
e o  1  11 1 x  21 2 ...x    p 1 p x  e o  2  12 1 x  22 2 ...x    p 2 p x  e o  3  13 1 x  23 2 ...x    p 3 p x
x 
x  
x
e  o 2   12 1  22 2 ...  p 2 p
 


... 
... 

... 
2    x  x   x    x  x   x    x  x   x
e o 1 11 1 21 2 p 1 p  e o 2 12 1 22 2 p 2 p  e o 3 13 1 23 2 p 3 p
x  
x 
x
e    13 1  23 2 ...  p 3 p
3
o
 

... 
... 

... 
2    x  x   x    x  x   x    x   x   x
e o 1 11 1 21 2 p 1 p  e o 2 12 1 22 2 p 2 p  e o 3 13 1 23 2 p 3 p
เช่นเดียวกันกับการวิเคราะห์ถดถอยโลจิสติกทวินาม ซึ่งเป็นการสร้างตัวแบบความน่าจะเป็นที่จะเกิด
เหตุการณ์เมื่อทราบตัวแปรพยากรณ์ จ าเป็นต้องมีการแปลงค่าความน่าจะเป็นดังกล่าวไปเป็น ตัวแปรจัด
ประเภท วิธีการหนึ่งที่ใช้กันมากและค่อนข้างง่ายตรง ๆ ไป ตรงมาคือการ assign แถวนั้น ๆ ไปยัง category